Найти площадь прямоугольного треугольника

Площадь треугольника по радиусу описанной окружности и трем сторонам

1 Общие формулы для вычисления площади треугольника

Формула площади треугольника по длине и высоте

S= a*h/2,
где а – это длина стороны треугольника, площадь которого нужно найти, h-длина проведенной к основанию высоты.

Формула Герона

S=√р*(р-а)*(р-b)*(p-c),
где √-это квадратный корень, p-полупериметр треугольника, a,b,c-это длина каждой стороны треугольника. Полупериметр треугольника можно вычислить по формуле p=(a+b+c)/2.

S = (a*b*sin(α))/2,
где b,c -это длина сторон треугольника, sin(α)- синус угла между двумя сторонами.

Формула площади треугольника по радиусу вписанной окружности и трем сторонам

S=p*r,
где p-это полупериметр треугольника, площадь которого нужно найти, r-радиус вписанной в этот треугольник окружности.

Формула площади треугольника по трем сторонам и радиусу описанной вокруг него окружности

S= (a*b*c)/4*R,
где a,b,c-это величина длины каждой стороны треугольника, R- радиус описанной вокруг треугольника окружности.

Формула площади треугольника по декартовым координатам точек

Декартовы координаты точек – это координаты в системе xOy, где x- это абсцисса, y- ордината. Декартовой системой координат xOy на плоскости называют взаимно перпендикулярные числовых оси Oх и Oy с общим началом отсчета в точке О. Если заданы координаты точек на этой плоскости в виде A(x1, y1), B(x2, y2) и C(x3, y3), то можно вычислить площадь треугольника по следующей формуле, которая получена из векторного произведения двух векторов.
S = |(x1 – x3)•(y2 – y3) – (x2 – x3)•(y1 – y3)|/2,
где || обозначает модуль.

Как найти площадь треугольника через высоту и основание

Теорема 1

Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.

Математически это выглядит следующим образом

$S=\frac{1}{2}αh$

где $a$ — длина стороны, $h$ — высота, проведенная к ней.

Доказательство.

Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.

Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда

$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$

Следовательно, искомая площадь треугольника, по свойству 2, равняется

$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$

Теорема доказана.

Пример 2

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Решение.

Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим

$S=\frac{1}{2}\cdot 9\cdot 9=40,5$

Ответ: $40,5$.

Самые крупные и полноводные реки России и их значение

Онлайн калькулятор

Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• длины катетов a и b
• длину гипотенузы с и длину любого из катетов (a или b)
• длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
• длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• длину гипотенузы с и один из острых углов (α или β)

Найти площадь прямоугольного треугольника по двум катетам

Катет a = Катет b = S =

Просто введите длины двух катетов, и получите ответ.

Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?

S = ½ ⋅ a ⋅ b

Пример

К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:

S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²

Найти площадь прямоугольного треугольника по катету и гипотенузе

Гипотенуза c = Катет (a или b) = S =

Введите длины гипотенузы и одного из катетов, и получите ответ.

Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?

S = ½ ⋅ a ⋅ √c² — a² = ½ ⋅ b ⋅ √c² — b²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:

S = 2 ⋅ √5² — 2² / 2 = √25 — 4 ≈ 4.58 см²

Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу

Катет (a или b) = Прилежащий угол (β или α) = ° S =

Введите длину одного из катетов и прилежащий к нему острый угол в градусах.

То есть к катету a прилежащий ∠β, а к катету b — ∠α

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?

S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:

S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²

Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу

Катет (a или b) = Противолежащий угол (α или β) = ° S =

Введите длину одного из катетов и противолежащий к нему острый угол в градусах.

То есть к катету a противолежащий ∠α, а к катету b — ∠β

Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?

S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:

S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²

Пример

К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:

S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²

Задача. Изменение площади при изменении длины сторон

Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?

Решение.

Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.

Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.

Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:

S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )  (см. первую строку рисунка внизу)

Длины сторон произвольного треугольника заданы переменными a, b, c.
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:

S₂ = 1/4 sqrt( ( 4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c) ) (см. вторую строку на рисунке внизу)

Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда

S₂ = 1/4 sqrt( 4 * 4 * 4 * 4 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — на третьей строке рисунка
S₂ = 1/4 sqrt( 256 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — четвертая строка

Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня    
S₂ = 16 * 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
S₂ = 4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) (см. пятую строку рисунка внизу)

Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.

S₂ / S = 16 (см. внизу подробнее запись в виде дроби и ее сокращения — в последней строке)

На рисунке логика вычисления решения, описанного выше, приведена уже в виде формул (одна за другой)

Ответ: Площадь треугольника увеличится в 16 раз

10380.6235
 

Сумма углов треугольникаОписание курса Медиана треугольника   

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Лето  —  прекрасное время, чтобы заниматься ей с удовольствием, в комфортном темпе, без контрольных и оценок за четверть, валяясь дома на полу или за городом на травке.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой. Наши преподаватели понятно объяснят что угодно  —  от дробей до синусов —  и ответят на вопросы, которые бывает неловко задать перед всем классом.

Биссектрисы треугольника

Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника:

1. Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.

2. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

   AEAB = ECBC

3. Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

   Угол между и ‘ = 90°

4. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

Качели-бревно

Высоты треугольника

Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

В зависимости от типа треугольника высота может содержаться

• внутри треугольника — для остроугольного треугольника;
• совпадать с его стороной — для катета прямоугольного треугольника;
• проходить вне треугольника — для острых углов тупоугольного треугольника.

Свойства высот треугольника

Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.

:: = 1:1:1 = ():():()

1 + 1 + 1 = 1

Как рассчитать площадь?

От качества выполнения работы по кровельному настилу зависит последующая комфортность проживания в жилом помещении. Чтобы правильно высчитать площадь крыши, нужно учесть тип и форму кровельного материала, а также особенности конструкции жилища. Точные вычисления позволяют сделать строение крыши надежным и прочным, определить количество денежных вложений.

Для этого могут быть использованы различные материалы, например, шифер, профнастил или металлочерепица, а также доборные комплектующие элементы. Листы кровли принято укладывать внахлест. Поэтому на каждую сторону крыши потребуется порядка 10-15% для продольного нахлеста.

Вычислить площадь кровли можно посредством выполнения необходимых замеров. При этом следует учитывать следующие факторы:

• площадь по углу наклона и геометрическому строению крыши;
• наличие на крыше люков и иных элементов, которые не будут покрыты кровельным настилом;
• выбранная теплоизоляция, тип утеплителя и облицовки.

Определение площади крыши предполагает вычисление высоты, угла наклона и объема стройматериалов. Грамотно рассчитав квадратуру, можно сэкономить на покупке кровли и транспортировке материалов. Однако следует закупать кровельные материалы с небольшим запасом во избежание их недостатка при монтаже или при допущении ошибок в укладке. При сложной конфигурации крыши с несколькими скатами придется рассчитать параметры геометрических фигур.

Площадь высчитывается по формуле в зависимости от формы ската:

• трапециевидный: (A+B) *H/2;
• прямоугольный: A*B;
• параллелограмм: A*H;
• равносторонний треугольник: (A*H) /2.

Где A – ширина кровли, B – длина кровли, H – высота треугольника.

Для простоты расчетов рекомендовано разделить сложные геометрические фигуры на простые элементы, а затем найти суммарную площадь полученных значений в квадратных метрах.

Для измерения площади треугольника фронтона нужно провести замеры длины торцевой стены и поделить ее пополам. Полученную величину умножить на tg угла, образуемого между скатом и основанием крыши.

Треугольный скат является наиболее распространенной геометрической конфигурацией домовладений. Ломаная разновидность крыши имеет более сложную конструкцию. Ее возведение затрудняется устройством стропильной системы и требуемыми расчетами.

Как найти площадь треугольника

Как вы можете помнить из школьной программы по геометрии, треугольник – это фигура, образованная из трех отрезков, соединяющихся тремя точками, не лежащими на одной прямой. Треугольник образует три угла, отсюда и название фигуры. Определение может быть и иным.

Треугольник можно так же назвать многоугольником с тремя углами, ответ будет так же верным. Треугольники делятся по числу равных сторон и по величине углов в фигурах.

Так выделяют такие треугольники, как равнобедренный, равносторонний и разносторонний, а так же прямоугольный, остроугольный и тупоугольный, соответственно.

Формул вычисления площади треугольника очень много. Выбирать, как найти площадь треугольника, т.е. какой формулой воспользоваться, только вам. Но стоит отметить лишь некоторые обозначения, которые используются во многих формулах вычисления площади треугольника. Итак, запоминайте:

S – это площадь треугольника,

a, b, c – это стороны треугольника,

h – это высота треугольника,

R – это радиус описанной окружности,

p – это полупериметр.

Вот основные обозначения, которые могут вам пригодиться, если вы совершенно забыли курс геометрии. Ниже будут приведены наиболее понятные и не сложные варианты вычисления неизвестной и загадочной площади треугольника. Это не сложно и пригодится как вам в домашних нуждах, так и для помощи своим детям в домашнем задании. Давайте вспомним, как вычислить площадь треугольника проще простого:

В нашем случае площадь треугольника равна: S = ½ * 2,2 см. * 2,5 см. = 2,75 кв.см. Помните, что площадь измеряется в квадратных сантиметрах (кв.см.).

Прямоугольный треугольник и его площадь

Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к.

сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника.

Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.

В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.

В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.

2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:

S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.

Равнобедренный треугольник и его площадь

Если перед вами стоит задача вычислить формулу равнобедренного треугольника, то проще всего воспользоваться главной и как считается классической формулой площади треугольника.

Но для начала, перед тем, как найти площадь равнобедренного треугольника, узнаем, что это за фигура такая. Равнобедренным треугольником называется треугольник, у которого две стороны имеют одинаковую длину. Эти две стороны называются боковыми, третья сторона называется основанием. Не путайте равнобедренный треугольник с равносторонним, т.е.

правильным треугольником, у которого все три стороны равны. В таком треугольнике нет особых тенденций к углам, точнее к их величине. Однако углы у основания в равнобедренном треугольнике равны, но отличаются от угла между равными сторонами.

Как вы можете заметить, в этих формулах активно используются углы, их величины, косинусы, синусы и тангенсы.

По этой причине, без специальной книжки вам не обойтись, хотя всю информацию вы сможете найти в Интернете.

Отметим только, что в формулах угол альфа – тот, что находится между боковой стороной и основанием, а угол гамма (y) – тот, что находится между равными боковыми сторонами треугольника.

Чертежи и размеры

Составляя чертежи садовых качелей, надо показывать их габариты в трех плоскостях. Начинают с суммарной ширины (которая определяется по фасадной части конструкции). Вторая цифра показывает, какова глубина каркаса. Третье число означает высоту. Нежелательно использовать большие качели в уличных навесах или беседках.

Но в любом случае требуется ориентироваться на особенности конкретного ландшафта или помещения, чтобы схема была составлена правильно

Если предстоит поставить качели просто под деревьями, где есть свободное место, можно обращать внимание на одну ширину. При этом стоит учитывать, что сиденье на 400-500 мм меньше, чем расстояние между боковыми стойками

Планируя сделать подвесную скамейку для семейной пары с 1 ребенком, можно ограничиться шириной 1,6 м. А вот для троих взрослых потребуется уже от 180 до 200 см.

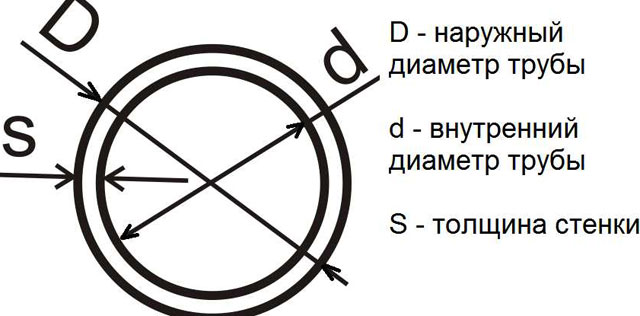
Точно такие же габариты стараются придать задним сиденьям автомобилей, так как они позволяют свободно рассаживаться всем без намека на стеснение. Если планируется пользоваться качелями в одиночку, хватит и сиденья шириной 1 м. Делать конструкцию крупнее — значит, уже тратить зря строительные материалы. В чертежах требуется отразить толщину круглых труб для изготовления стоек и иных деталей. Их диаметр может варьироваться от 3,8 до 6 см.

Допустимая толщина стенок колеблется от 0,1 до 0,15 см. Увеличивая эти показатели, можно нарастить прочность. Однако общая плата тоже существенно вырастает. В частном саду уместно монтировать качели из трубы сечением 3,8-4,5 см. При этом толщина трубки может ограничиться 1,2 мм. Более серьезные параметры нужны уже для качелей, вывешиваемых в общественных местах.

На чертеже А-образного каркаса указывают:

• фланцы;
• рым-гайки;
• простые гайки;
• болты;
• стягивающие раму элементы;
• перекладины;
• стойки опорных рам.

Как вычислить площадь треугольника

Треугольник – это такая геометрическая фигура, которая состоит из трех прямых, соединяющихся в точках, не лежащих на одной прямой.

Точки соединения прямых – это вершины треугольника, которые обозначаются латинскими буквами (например, A, B,C).

Соединяющиеся прямые треугольника называются отрезками, которые также принято обозначать латинскими буквами. Различают следующие типы треугольников:

• Прямоугольный.
• Тупоугольный.
• Остроугольный.
• Разносторонний.
• Равносторонний.
• Равнобедренный.

1

Общие формулы для вычисления площади треугольника

Формула площади треугольника по длине и высоте

S= a*h/2,где а — это длина стороны треугольника, площадь которого нужно найти, h-длина проведенной к основанию высоты.

Формула Герона

S=√р*(р-а)*(р-b)*(p-c),где √-это квадратный корень, p-полупериметр треугольника, a,b,c-это длина каждой стороны треугольника. Полупериметр треугольника можно вычислить по формуле p=(a+b+c)/2.

Формула площади треугольника по радиусу вписанной окружности и трем сторонам

S=p*r,где p-это полупериметр треугольника, площадь которого нужно найти, r-радиус вписанной в этот треугольник окружности.

Формула площади треугольника по трем сторонам и радиусу описанной вокруг него окружности

S= (a*b*c)/4*R,где a,b,c-это величина длины каждой стороны треугольника, R- радиус описанной вокруг треугольника окружности.

Формула площади треугольника по декартовым координатам точек

Декартовы координаты точек – это координаты в системе xOy, где x- это абсцисса, y- ордината. Декартовой системой координат xOy на плоскости называют взаимно перпендикулярные числовых оси Oх и Oy с общим началом отсчета в точке О.

Если заданы координаты точек на этой плоскости в виде A(x1, y1), B(x2, y2) и C(x3, y3), то можно вычислить площадь треугольника по следующей формуле, которая получена из векторного произведения двух векторов.

S = |(x1 – x3)•(y2 – y3) – (x2 – x3)•(y1 – y3)|/2,

где || обозначает модуль.

https://youtube.com/watch?v=ayOt9DwAsSQ

Прямоугольный треугольник – это такой треугольник, у которого один угол составляет 90 градусов. Такой угол у треугольника может быть лишь один.

Формула площади прямоугольного треугольника по катету и противолежащему углу

S = a*b/2*tg(β),где a, b – это катеты треугольника, tg(β) – это тангенс угла, в котором соединяются катеты a, b.

3

Как вычислить площадь равнобедренного треугольника

Равнобедренным называется такой треугольник, который имеет две равные стороны. Эти стороны называются боковыми, а другая сторона является основой. Для вычисления площади равнобедренного треугольника можно использовать одну из следующих формул.

Формула равнобедренного треугольника по боковой стороне и основанию

S=(c/2)* √(a*a – c*c/4),где с – основание треугольника, a- величина одной из боковых сторон равнобедренного треугольника.

Как найти площадь равностороннего треугольника

Равносторонний треугольник – это такой треугольник, у которого все стороны равны. Для вычисления площади равностороннего треугольника можно использовать следующую формулу: S = (√3*a*a)/4,

где a-это длина стороны равностороннего треугольника.

Вышеприведенные формулы позволят вычислить искомую площадь треугольника

Важно помнить, что для вычисления пощади треугольников нужно учитывать тип треугольника и доступные данные, которые можно использовать для вычисления

Из чего можно сделать качели своими руками

Обустраивая места для проведения досуга, позаботьтесь о появлении в них удобных и практичных качелей. Не спешите отправляться за ними в магазин. Попробуйте сделать дачные качели своими руками. Из чего? Из того, что попадется под руку. А что всегда найдется на дачном участке?

Канат

Это основной элемент конструкции знаменитой «тарзанки», способной вызывать вопли восторга не только у детей, а и у весьма солидных взрослых дядей, рискнувшись на ней прокатиться. Чаще всего ее располагают над водоемами и параллельно наделяют функцией своеобразного трамплина для прыжков в воду.

качель из каната и бревнышка

Соорудить веревочный вариант не трудно. Все, что потребуется, это подыскать попрочнее ветку и привязать к ней один конец каната. С другой стороны завязывается толстый узел или привязывается небольшой толщины отшлифованное бревнышко, за которое будет приятно и удобно хвататься руками.

Древесина

Это материал, из которого можно сделать менее легкомысленные качели на даче своими руками. У деревянных конструкций должно быть комфортное сидение. К преимуществам подобного варианта стоит отнести экологичность изделия. Деревянная модель просто впишется в любой садовый ландшафт, независимо от его стилистического решения.

такие детские качели сможет смастерить даже новичок в столярном деле

Дерево – не слишком сложный материал в работе, поэтому использовать его на создание качелей могут даже новички в столярном деле. Как сделать качели на дачу из дерева, мы расскажем чуть ниже, а пока отвлечемся на его недостатки.

При том, что материал считается прочным, он не является долговечным и плохо реагирует на влагу, холод, солнечные лучи. Продлить срок службы деревянной качели можно, только обработав ее защитными составами, которых сегодня, благо, в изобилии.

Металл

Качели своими руками из металла сделать смогут лишь избранные, то есть те, кто имеет опыт работы со сваркой или знают кузнечное дело. Безусловно, металлические модели наиболее прочны и рациональны для использования на открытом воздухе. Их можно сделать:

1. Разборными.
2. Мобильными.
3. Стационарными.

стеклянные качели следует устанавливать в тенистом месте

По способу производства они также разделятся на:

• сварные;
• кованые.

Качели ручной ковки выделяет роскошный и богатый экстерьер. Ажурные элементы придают дачным качелям уникальность и делают их стильным дополнением ландшафтного дизайна. Если вам нужны вечные качели на даче – сделайте их именно из металла.

Естественно, металлическую поверхность каркаса придется также защищать специальным покрытием (при условии, что вы не сварили качели из нержавейки), что можно отнести к недостаткам материла. Но по большому счету недостаток у металлических конструкций лишь один и тот относительный. Речь об их массивности. Большой вес усложняет задачи по перемещению мобильных и разборных вариантов.

Пластик

качель, выполненная в виде корзины

Не знаете, как сделать детские качели для улицы – обратите внимание на прочные полимеры. Возможно, сидение придется купить, а быть может, нечто подходящее на эту роль отыщется в закромах сарая

Проше всего соорудить подвесные детские качели. Для этого варианта достаточно будет пропустить сквозь отверстия или заправить в пазы веревку и приспособить всю конструкцию на дерево или опору иного вида. Для малышей все-таки рациональнее приобретать готовые качели из пластика. В принципе стоят они не так уж и дорого, но зато выглядят очень привлекательно. Они ярки, не реагируют на влагу, не нуждаются в специфическом уходе.

При выборе конструкции обращайте внимание ка качество пластика. Он не должен при нагреве выделять токсинов

оригинальные пластиковые качели треугольной формы

Пластиковые качели на даче могут не всегда гармонично сочетаться с окружающим пейзажем. Современность материала может свести на нет все усилия дизайнера по приданию ландшафту винтажного или деревенского вида. Нельзя назвать положительным и тот факт, что пластиковые качели – аттракцион не для всей семьи. Покататься на них не смогут ни подростки, ни взрослые.

И еще. В качелях для дачи, собранных своими руками, вполне может проскочить симбиоз материалов. Это не будет казаться нонсенсом. Дерево может стать чудесным дополнением металла, а канат – дерева.

По наличию осей подвижности

Обязательное условие любого элемента декора – вместительность и проходимость. Качели для дачи не должны мешать хозяевам, а также обязаны быть полностью безопасными для малышей. Поэтому придумано несколько видов конструкций данного типа:

• Одна ось. Наиболее простая сборка, легкая даже для детей, качающаяся только вперед-назад. Но, если школьники орудуют веревкой и крепкой веткой, то взрослый сможет сварить железного зверя. Данные качели можно обезопасить специально спинкой и отделениями для маленьких детских ножек.
• 2 оси. Любимый вид сооружения для детей школьного и дошкольного возраста, качающаяся вперед-назад, а также вправо-влево.
• С одной подвесной точкой. Эта конструкция висит на 1 веревке, что позволяет ей вращаться в разные стороны. Подходит для домашнего украшения или предмета отдыха – подвесное кресло выглядит довольно красиво и уютно.

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами и основанием

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

+ + = 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если > , тогда >

если = , тогда =

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

+ > + > + >

Стороны треугольника пропорциональны синусам противолежащих углов.

	=		=		= 2R

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

2 = 2 + 2 — 2·

2 = 2 + 2 — 2·

2 = 2 + 2 — 2·

Заключение